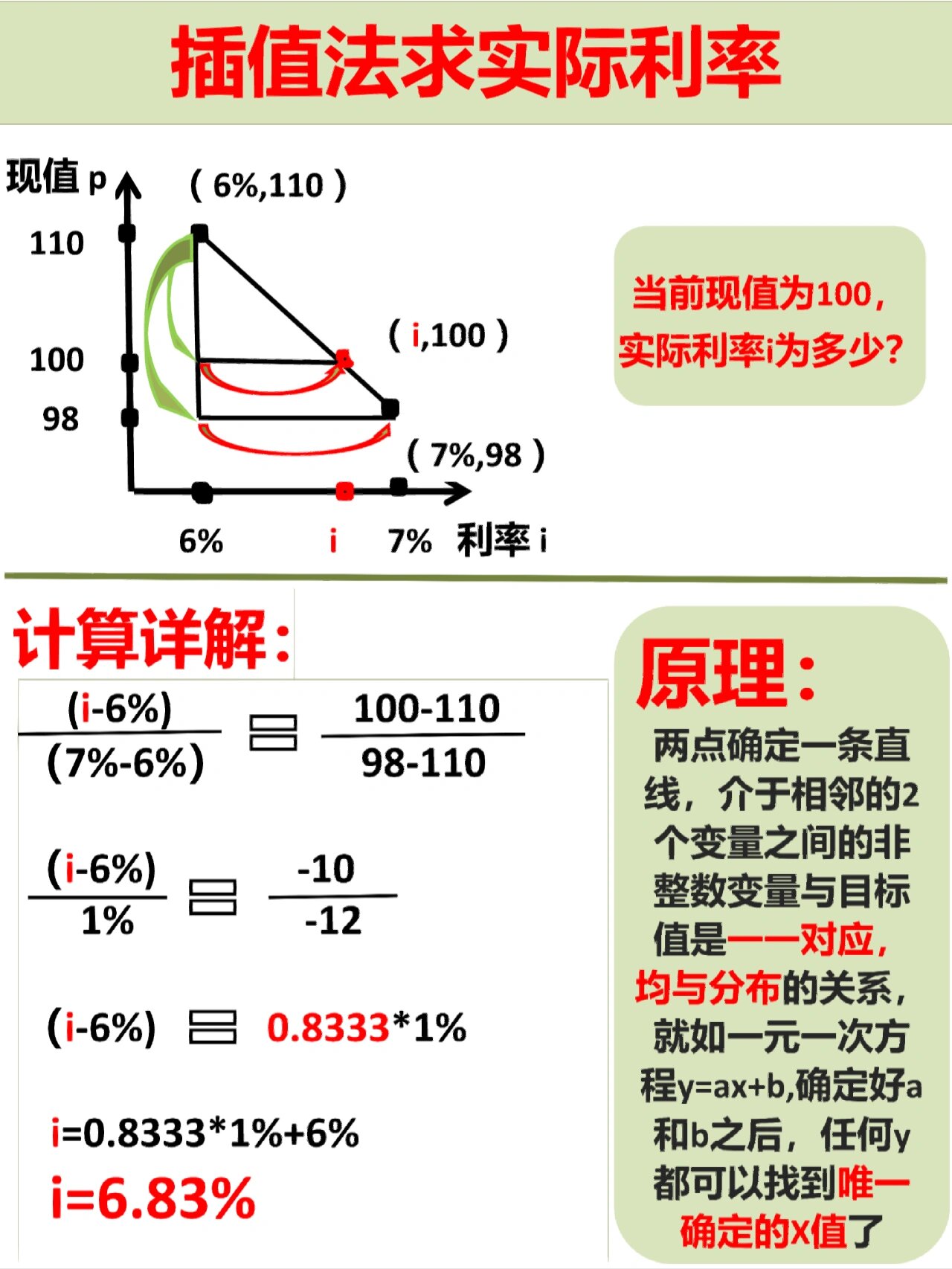
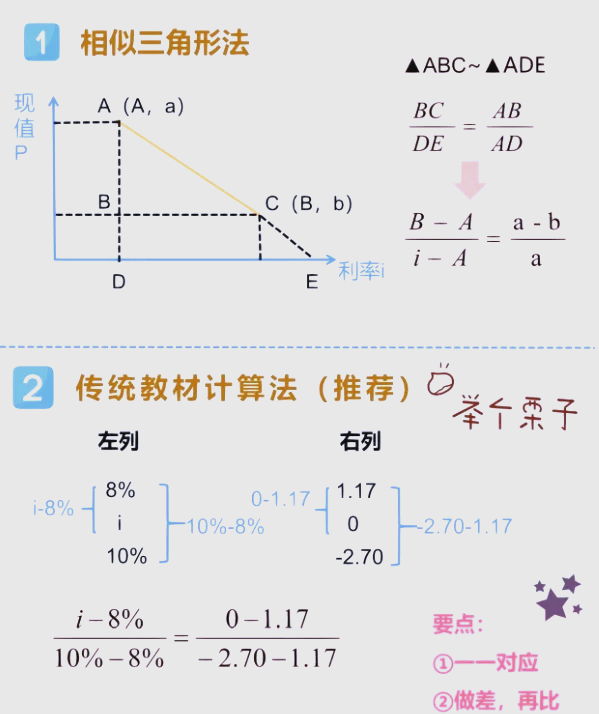
插值法求利率

100=13.8*(P\/A,i,10)(P\/A,i,10)=100\/13.8=7.246 6% 7.360 i 7.246 8% 6.710 (i-6%)\/(8%-6%)=(7.246-7.360)\/(6.710-7.360)i=6.35

如何计算百分位数,要求详细举例说明

首先确定位置：(10-1) * 75 \/ 100 = 7.35。因此，第75百分位数位于第7.35个位置，即70和80之间的位置。根据线性插值法，第75百分位数为70 + 0.35*(80-70) = 77.5。通过以上例子，我们可以看到，计算百分位数不仅可以帮助我们更好地理解数据分布情况，还能在数据分析中发挥重要作用。

什么是内插值法,举个实例来说明

插值法是函数逼近的一种重要方法，是数值计算的基本课题。本节只讨论具有唯一插值函数的多项式插值和分段多项式插值，对其中的多项式插值主要讨论n次多项式插值的方法，即给定n+1各点处的函数值后，怎样构造一个n次插值多项式的方法。虽然理论上可以用解方程组（2）（那里m=n）得到所求插值多项式，但遗憾...

轴肩理论用力系数,怎么使用插值法求,举个实例,比如当D\/d=1.16,r\/d=...

要准确的话可用图形法，把前后有值的坐标画出来，连接成闭合区域，在找你要的坐标位置。不过一般用线性插值法就行了！如，弯曲：先找r\/d=0.04,D\/d=1.2；1.1的直线，找点r\/d=0.04,D\/d=1.16的值；后再用线性插值找r\/d=0.048,D\/d=1.16就行了！

为什么采用插值法

三、插值法的实际操作简便性 插值法的操作相对简便，不需要复杂的数学建模和计算。通过选择适当的插值方法，如线性插值、多项式插值等，可以快速构建出估算函数，对未知数据进行估算。四、插值法的实际案例应用 在实际应用中，插值法广泛应用于各个领域。例如，在气象学中的天气预报，通过已知的气象数据点...

内插法的计算方法是什么

用内插法的话首先要找一个比14.8KM大的一个数，就选择15KM吧，则其对应的价格为54元则对应关系为：18 5 X 14.8 54 15 列得算式：(54-X)\/(15-14.8)=（X-18）\/（14.8-5）解得X=53.28元 应用内插法求值的条件：1、必须确知与所求变量值（x）左右紧密相邻变的两组变量...

数值分析:数值积分(插值法)

多元函数积分：对于二元函数的重积分，可以将其化为累次积分，从而将复杂的问题转化为多个一元函数积分的求解。在矩形积分区域，可以使用复合辛普森公式或其他方法来数值计算。综上所述，数值积分中的插值法提供了多种近似计算复杂函数积分的有效工具，展示了数值分析在处理实际问题中的强大能力。

拉格朗日插值算法

Z　 输入参数，两维实数组，容量为N×2，存放给定的插值节点数列及对应的观测值。N输入参数，整变量，插值节点数。NJ　 输入参数，整变量，插值节点数。CZ　 输入输出参数，二维实数组，容量NJ×2，第一列输入插值点数列，第二列输出插值 结果。计算实例 （1）、例题 设已知下表观测数据 x...

拉格朗日插值方法的理论基础。

然而，实际应用中，处理大量数据时需要谨慎。例如，对于一年365天的营收数据，我们通常只需考虑缺失数据前后几天的数据，以构建适当的插值函数，避免过度拟合导致的“龙格现象”。在Python中实现拉格朗日插值，我们将在后续文章通过实例讲解。总的来说，拉格朗日插值法是数据处理中解决缺失值问题的有力工具，但...

债券内在价值怎么计算?

债券内在价值计算需要用内插法（又叫插值法）计算，也就是根据比例关系建立一个方程，然后，解方程计算得出所要求的数据。一、决定债券内在价值的主要变量：决定债券内在价值的主要变量是债券期值、债券偿还期、市场收益率。1、债券内在价值计算步骤为计算各年的利息现值并加总得利息现值总和;2、计算债券...