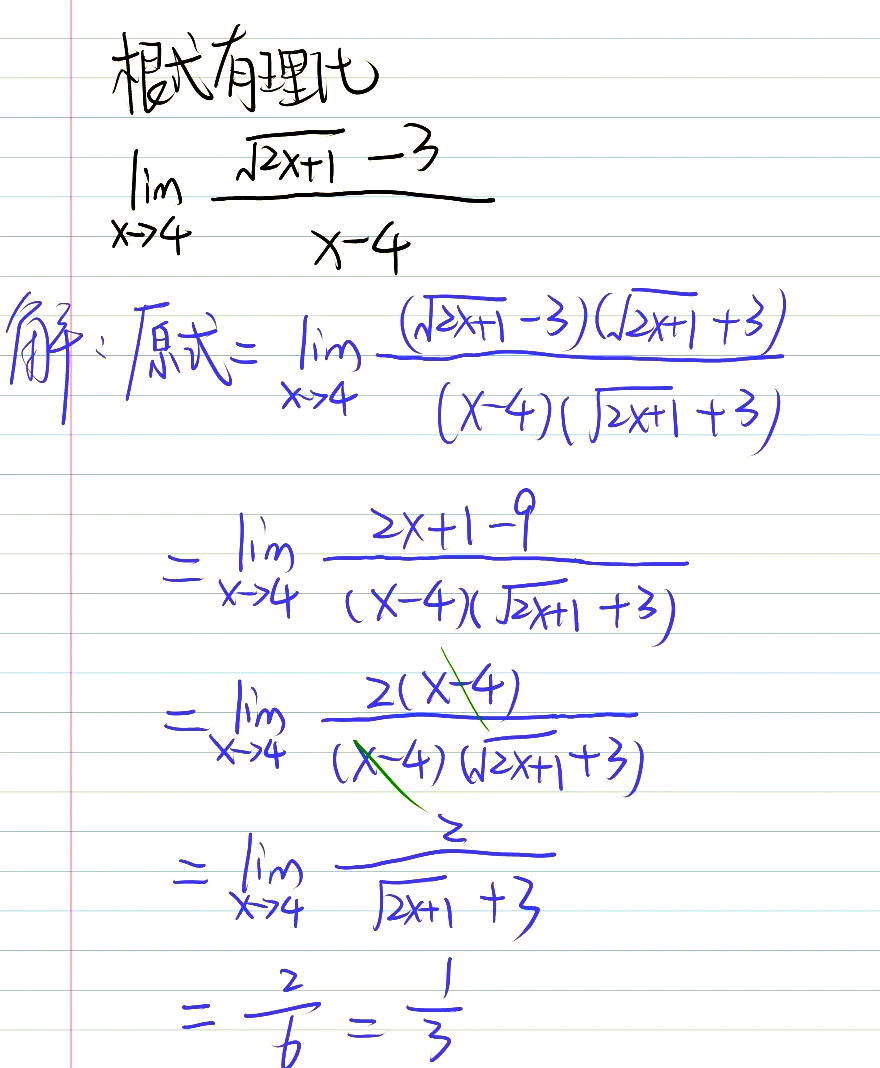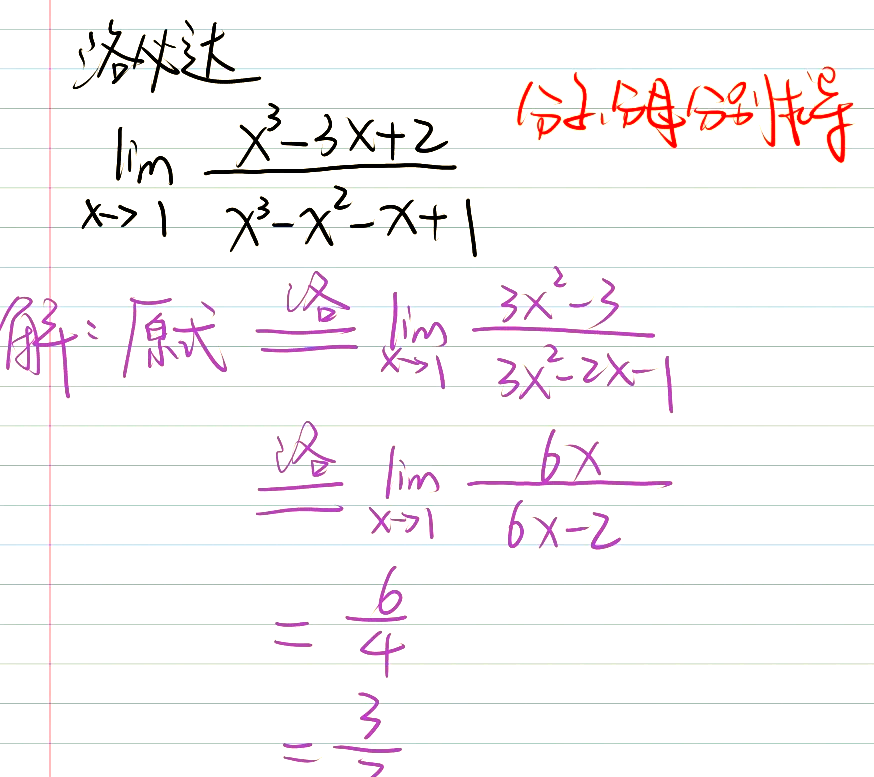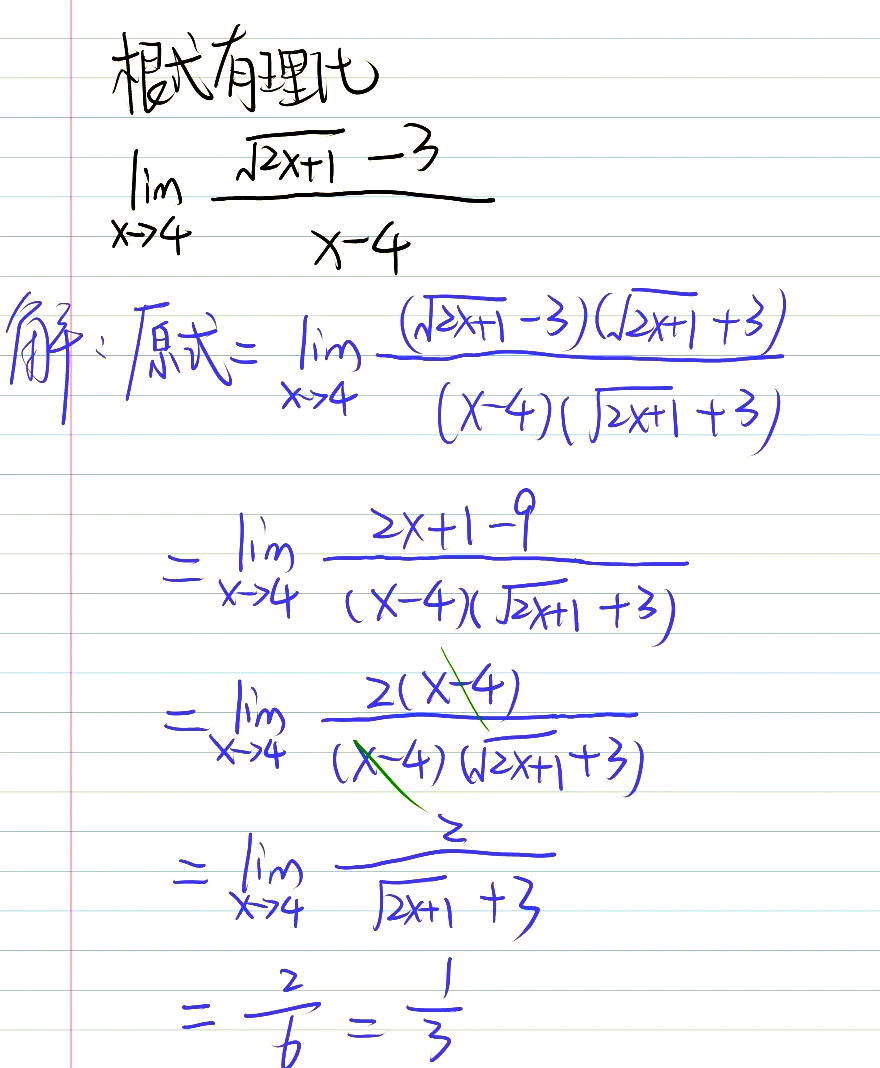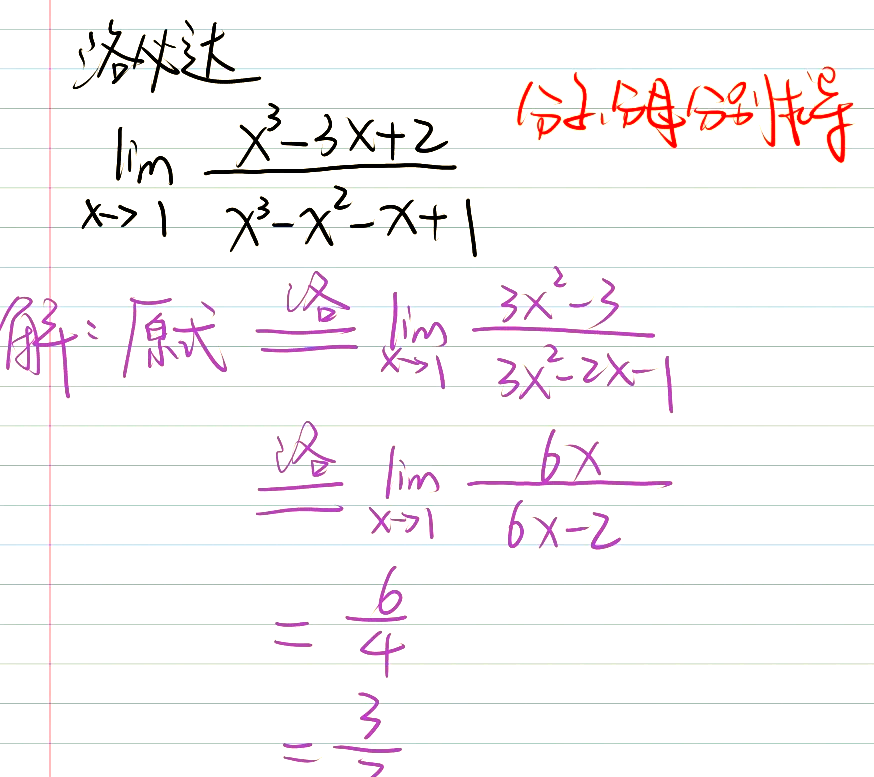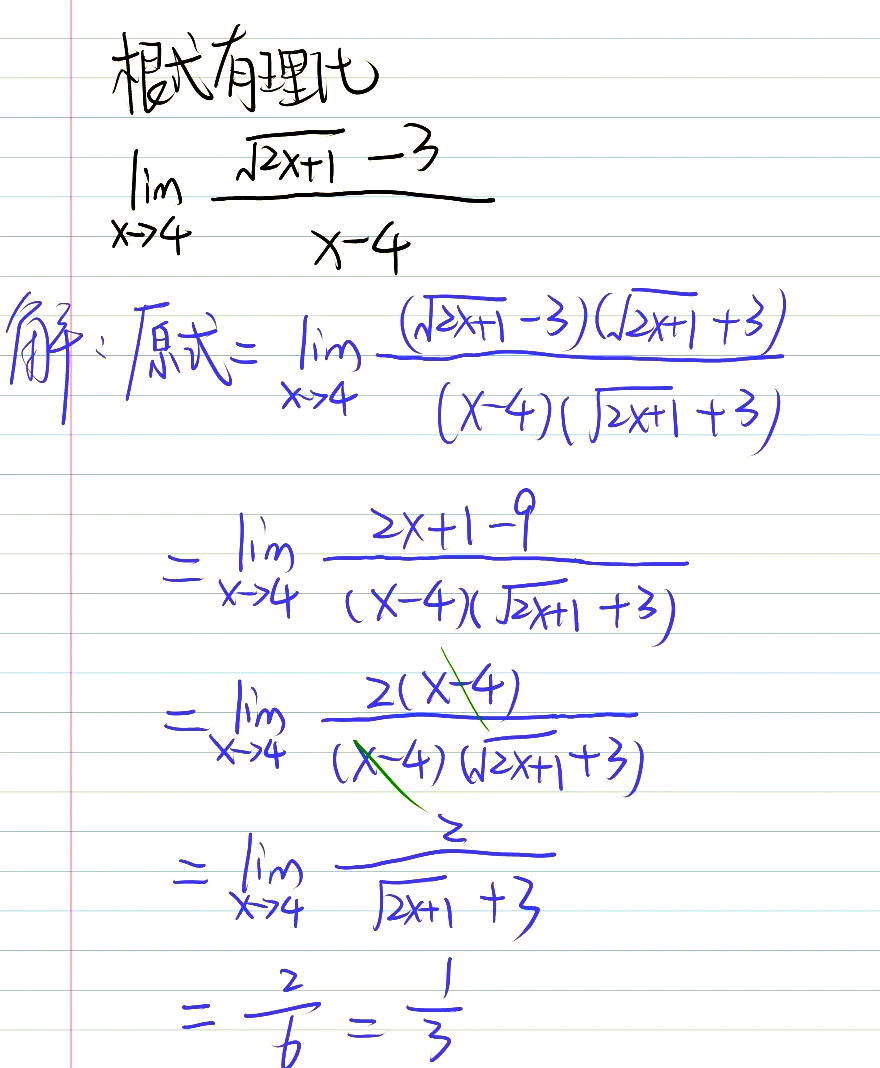
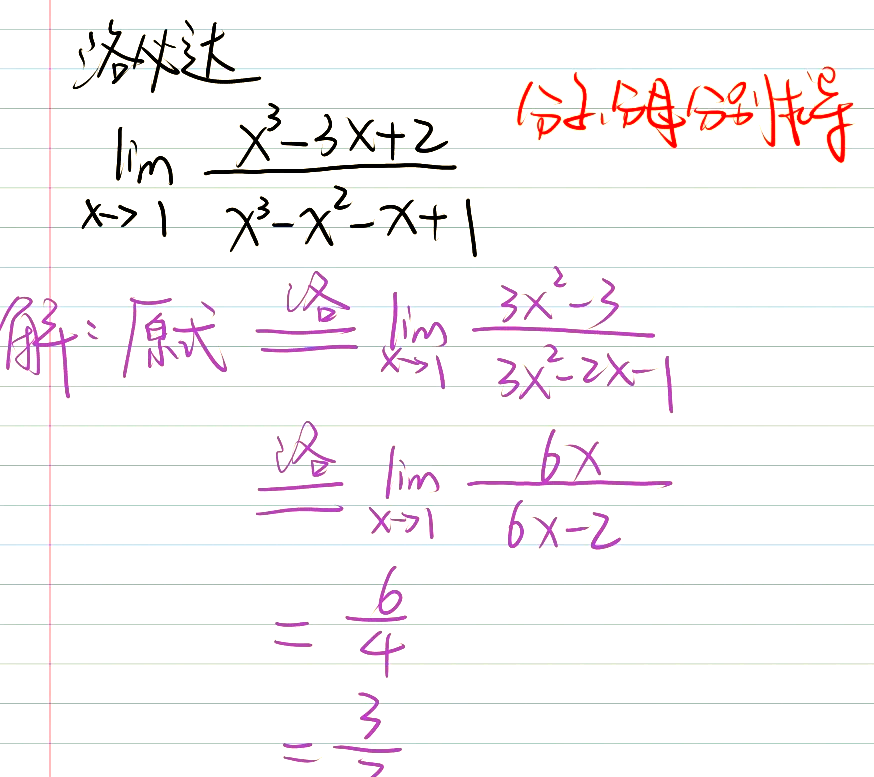
0除0的极限三种方法

其中A大于0，α大于等于2，β大于0为实数，那么我们有limx→x0f(x)g(x)=1。这种方法对于求常见的0除0型极限非常有效。当使用洛必达法则求limx→x0f(x)g(x)变得复杂时，使用该方法可以简化计算过程。第二种方法是因式分解法。通过因式分解来约去零因式，从而将未定式转化为普通的极限问题。这种方法特别适用于多

左极限是0-还是0+?

左极限是0-。0+和0-是不同的，例如f(x)=|x|，x趋于0-时，指x从左边趋于0，实际x是小于0，故f（x）=-x；x趋于+时，指x从右边趋于0，实际x是大于0，故f（x）=x。0+位于原点的右侧，0-位于原点的左侧，0+是右极限，0-是左极限。又因为ε是任意小的正数，所以ε\/2、3ε、ε2等也...

0\/0型极限怎么求

利用洛必达法则与等价无穷小代换对抽象函数的00型极限可得结论：设当x→x0时f（x）与g（x）为无穷小,g（x）～（x-x0）β，取k为正实数，使得fk（x）=A（x-x0）α＋o[（x-x0）α]。其中A〉0，α≥2，β〉0为实数，则有limx→x0f（x）g（x）=1。该方法对求常见的00型极限都...

请问x趋于0+的计算方法?

x趋向于0+和0-的计算应注意什么？计算的时候，要注意的就是正负号的问题。比如：当x→0 +时候，lim= 1；当x→0 -时候，lim= -1。两者都是无限趋近于零，只不过x→0 +是正值，x→0 -是负值，比如求1\/x在x→0 +的极限，就是正无穷大，x→0 -是负无穷大，x→0就就无穷大（就是包括...

0+和0-的区别

1. "0+"和"0-"分别代表数学中函数在某一点处右侧和左侧的极限值，它们的区别在于接近该点的方向不同。2. 具体来说，假设函数f(x)在某一点a处有定义。当我们研究f(x)在a点右侧的趋势时，取一个比a稍大的数x，并计算序列{f(x)}的极限值。这个极限值就是f(x)在a点右侧的"0+"极限。3....

极限趋向于0正和0负怎么算

2、0正和0负的计算方法：如果求极限时出现无穷，直接倒代换就行了，不用想太多。只要考虑倒代换后的0的正负。删掉符号后记得用绝对值处理!。3、0加和0减的比较：0正和0负的极限值可能不同，例如f（x）等于|x|，x趋于0负时，指x从左边趋于0，实际x是小于0，故f（x）等于负x；x趋于正时，...

怎么求0\/0型极限呢?

如果能够将f(x)转化为其他形式，一般就可以求得极限。2. 利用泰勒级数展开：将函数f(x)在x=a处展开成幂级数形式，然后利用级数展开的性质，将f(x)进行简化和变形。如果能够去掉分母中的零项，可以得到一个不再是0\/0型的形式，进而求得极限。需要注意的是，在求解0\/0型极限时，有时会遇到一些...

0\/0型极限怎么求

这一方法广泛应用于求解常见的0\/0型极限。当使用洛必达法则直接求解limx→x0f（x）\/g（x）较为复杂时，该方法可以简化计算过程。通过合理的代换和变换，可以更容易地找到极限值，提高解题效率。需要注意的是，在应用该方法时，应确保代换后的函数形式满足条件，即fk（x）=A（x-x0）α＋o[（x-...

极限0\/0型怎样处理?

1.可以运用罗毕达法则，但是罗毕达法则并非万能。例如，当x趋向于0时，sinx\/根号（1-cosx ），就是0\/0型。2.可以用等价无穷小代换，但是这个方法是从麦克劳林级数、或泰勒级数。3.麦克劳林级数、泰勒级数展开法，这是万能的，只是稍微麻烦一点。4.运用重要极限sinx\/x。5.简化0\/0的不定式计算，成为...

极限的0_0是什么意思

0+ 、0_都是极限意义 正号 表示从正向（右到左）趋向。0+ 即为左极限 负号 表示从负向（左到右）趋向。0-即为右极限 这种趋向可通过函数图像判断 而如果函数图像较复杂，则需要分别判断，一般考虑不同的趋向 使结果趋向 正负、无穷、常数等 ...