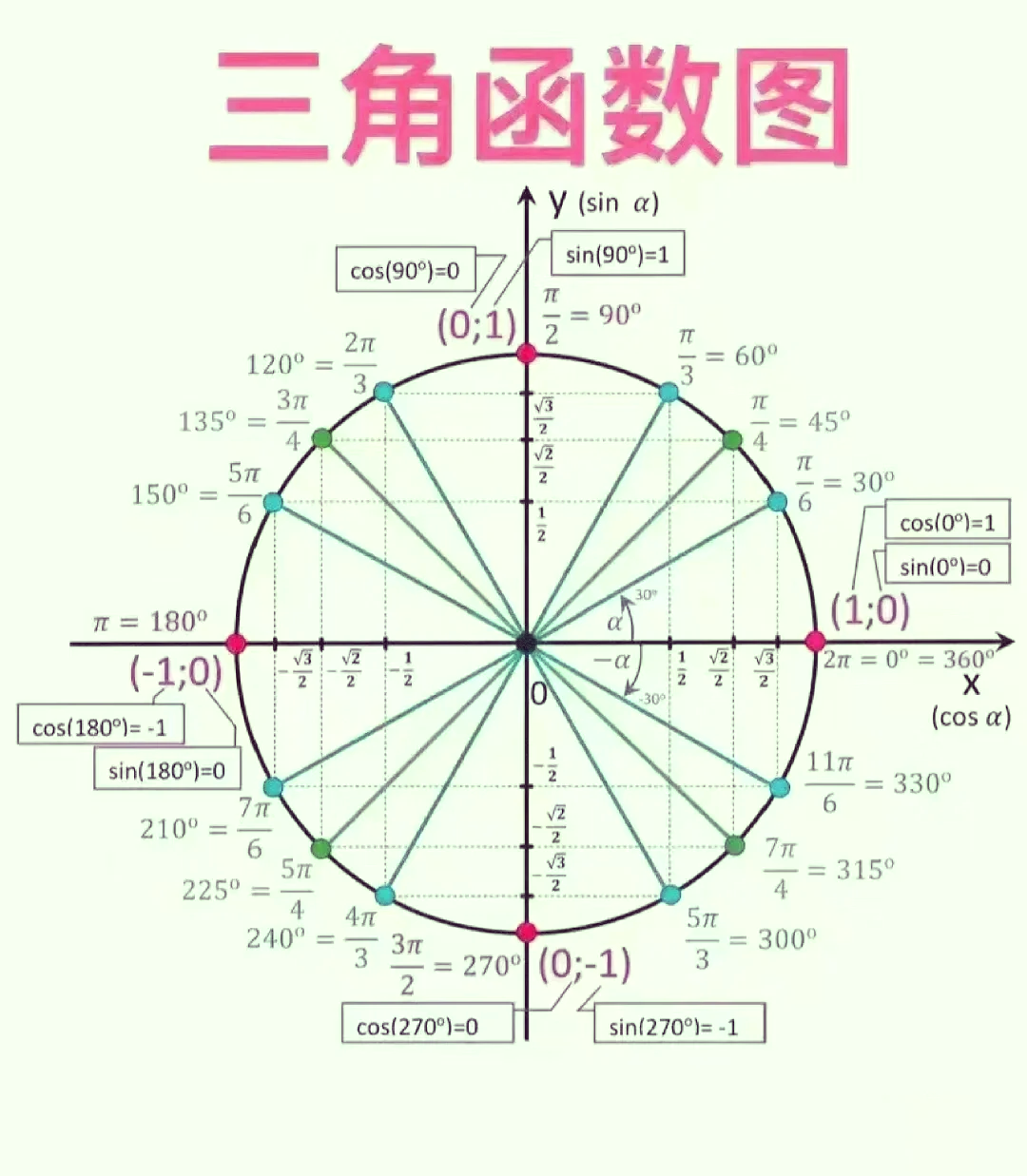
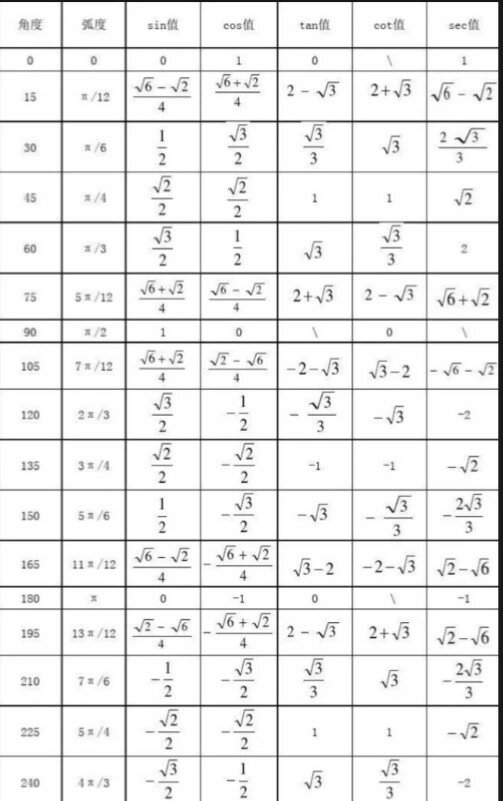
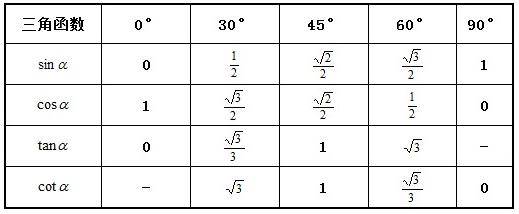
三角函数sin,cos,tan。

再用和差角公式计算 例：方法一：sin(24°15’)=sin(24.25π\/180)=sin(97π\/720)≈sin(0.4232423)≈ 0.4232423 - 0.4232423^3\/(1×2×3) + 0.4232423^5\/(1×2×3×4×5) - 0.4232423^7\/(1×2×3×4×5×6×7)≈0.41 方法二：sin(24°15’)

数学公式

97性质定理2相似三角形的周长比等于相似比 98性质定理3的面积的比例相似?一个三角形的相似比的平方等于 99任意的正弦值的锐角等于互补的角度的余弦值,任何急性夹角余弦 其互补的角度的正弦值 100的任何锐角的正切值等于其互补角的余切余切任何锐角值的 互补的角度的正切 圈是101中的一个点的距离相等的长度的点的...

初中数学

绝对值:①在的轴的数量,被称为从原点的距离的点相对应的数目的若干的绝对值。 (2)绝对值本身的正数,负数的绝对值是他的相反数,0的绝对值是0。两个负的相对大小,而不是绝对值。 有理数的运算:加法:①连号总和,采取同样的符号,绝对值的总和。 ②添加不同的症状和绝对值相等的值,并是0;不平等的绝对值,...

求三角形高的公式

3、钝角三角形：三角形的三个内角中有一个角大于90度。判定法二：1、锐角三角形：三角形的三个内角中最大角小于90度。2、直角三角形：三角形的三个内角中最大角等于90度。3、钝角三角形：三角形的三个内角中最大角大于90度，小于180度。其中锐角三角形和钝角三角形统称为斜三角形。

三角诱导公式是什么,有哪些。

所谓三角函数诱导公式，就是将角n·(π\/2)±α的三角函数转化为角α的三角函数。公式一 sin(2kπ+α)=sinα cos(2kπ+α)=cosα tan(2kπ+α)=tanα cot(2kπ+α)=cotα sec(2kπ+α)=secα csc(2kπ+α)=cscα (k∈Z)公式二 sin(π+α)=-sinα cos(π+α)=-cosα tan(...

已知tan=-2,则sina*cos的值为多少

设直角三角形内三边分别为a、b、c，a的对边是角a，则sina=a\/c,cosa=b\/c,tana=a\/b,由此得出tana=sina\/cosa.

初中数学

35推论1的三个角是相等的三角形是正三角形，36推论2有一个角等于60 °的等腰三角形是等边三角形 37在一个直角三角形，锐角等于30°，因此它的直角??边缘等于斜边半 38直角三角形等于斜边上的中线等于斜边 39定理段垂直平分线点的一半，和本段的两个端点的距离 40组相反的，所有的点和线的两个...

数学公式

?选区采取的最好按逆时针顺序从右上角,这样的结果一般都是做出来的时候,如果你不采取这个规则,可能为负,但不要紧,只要的它的绝对值不影响的面积的大小?一个三角形! 】 ? 霍纳三角形中线面积公式 ?S =√[(MA + MB + MC)*(MB + MC-马)*(MC +麻MB)*(MA + MB-MC)] \/ 3 ?其中MA,MB,MC三角形...

已知等腰三角形底边长和高,如何计算顶角?

所以底边的一半=x÷2 再利用三角函数tanA=（x÷2）÷y （设A为顶角的一半，因为在等腰三角形中，底边上的高线为顶角平分线）（tanA=对边÷临边，即等腰三角形（底边的一半）÷底边上的高，具体的A的值可以将x、y的具体数值带入后，用计算器或其他方法求得）所以顶角的度数=2A （A为上式tanA=...

如图,以三角形abc的一边ab为直径作圆o,圆o与bc边的交点d恰好为bc的中...

由此可得od和ac平行 de是切线，od是半径则两者垂直，从而，de和ac垂直（垂直于平行线中的一条的也和另一条垂直）2.连接ad，设圆0的半径为r，因为AB是直径所以ADB是一直角三角形，角B是30度，可得bd =r根号3，cb=cd+bd=2bd =2r根号3 过o点作cb垂线交于h则bh0.5r根号3，oh=o.5r，ch=...